탐색 연산
1. 탐색 연산의 기본 방법
- 연산 방법
▪ 루트에서 시작함
▪ 탐색할 키 값 x를 루트 노드의 키 값과 비교함
* 키 값 x = 루트 노드의 키 값 인 경우
=> 원하는 원소를 찾았으므로 탐색 연산 성공
* 키 값 x < 루트 노드의 키 값 인 경우
=> 루트 노드의 왼쪽 서브 트리에 대해서 탐색 연산 수행
* 키 값 x > 루트 노드의 키 값 인 경우
=> 루트 노드의 오른쪽 서브 트리에 대해서 탐색 연산 수행
▪ 서브 트리에 대해서순환적으로 탐색 연산을 반복함
2. 탐색 연산 알고리즘
1) 이진 탐색 트리에서의 탐색 연산 알고리즘
searchBST(bsT, x)
p ← bsT;
if (p = null) then
return null;
if (x = p.key) then
return p;
if (x < p.key) then
return searchBST(p.left, x);
else return searchBST(p.right, x);
end searchBST( )3. 탐색 연산 예제
1) 원소 11 탐색하기


▪ 예제: 이진 탐색 트리에서의 탐색 과정
① 찾는 키 값 11을 루트 노드의 키 값 8과 비교(찾는 키 값 11 > 노드의 키 값 8)이므로, 오른쪽 서브 트리를
탐색함
② 찾는 키 값 11 < 노드의 키 값 10)이므로, 다시 오른쪽 서브
트리를 탐색함
③ (찾는 키 값 11 < 노드의 키 값 14)이므로, 왼쪽 서브 트리를
탐색함
④ 찾는 키 값 11 = 노드의 키 값 11이므로, 탐색 성공!
(연산 종료)
삽입 연산
1. 삽입 연산의 기본 방법
- 연산 방법
① 먼저 탐색 연산을 수행
▪ 삽입할 원소와 같은 원소가 트리에 있으면 삽입할 수 없으므로, 같은 원소가 트리에 있는지 탐색하여 확인함
▪ 탐색에서 탐색 실패가 결정되는 위치가 삽입 위치가 됨
② 탐색 실패한 위치에 원소를 삽입함
2. 삽입 연산 알고리즘
1) 이진 탐색 트리에서의 삽입 연산 알고리즘
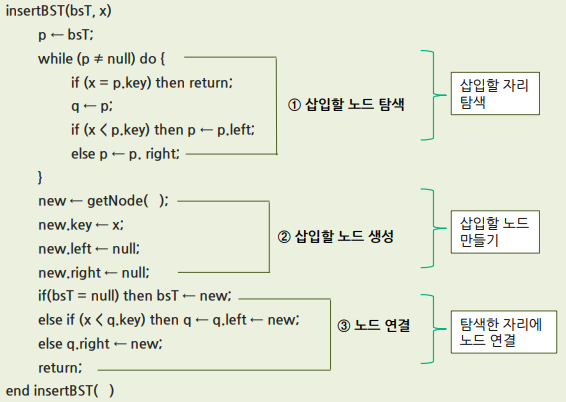
3. 삽입 연산 예제
1) 원소 4 삽입하기
▪ 예제 - 삽입할 위치 탐색



① 찾는 키 값 4를 루트 노드의 키 값 8과 비교하여(찾는 키 값 4 < 노드의 키 값 8)이므로, 왼쪽 서브 트리를 탐색함
② (찾는 키 값 4 > 노드의 키 값 3)이므로, 오른쪽 서브 트리를 탐색함
③ (찾는 키 값 4 < 노드의 키 값 5)이므로, 왼쪽 서브 트리를 탐색해야
하는데, 왼쪽 자식 노드가 없으므로 탐색 실패!
이 때 탐색 실패가 결정된 위치, 즉 왼쪽 자식 노드의 위치가 삽입 위치가 됨
④ 탐색 작업으로 찾은 자리, 즉 노드 5의 왼쪽 자식 노드 자리에 노드 4를 삽입함
삭제 연산
1. 삭제 여산의 기본 방법
- 연산 방법
① 먼저 탐색 연산을 수행
▪ 삭제할 노드의 위치를 알아야 하므로 트리를 탐색함
② 탐색하여 찾은 노드를 삭제함
▪ 노드의 삭제 후에도 이진 탐색 트리를 유지해야 하므로 삭제 노드의 경우에 대한 후속 처리(이진 탐색 트리의 재구성 작업)가 필요함

2. 삭제 연산 알고리즘
1) 이진 탐색 트리에서의 삭제 연산 알고리즘
deleteBST(bsT, x)
p ← 삭제할 노드;
parent ← 삭제할 노드의 부모 노드;
if (p = null) then return; // ① 삭제할 노드가 없는 경우
if (p.left = null and p.right = null) then { // ② 삭제할 노드의 차수가 0인 경우
if (parent.left = p) then parent.left ← null;
else parent.right ← null;
}
else if (p.left = null or p.right = null) then { // ③ 삭제할 노드의 차수가 1인 경우
if (p.left ≠ null) then {
if (parent.left = p) then parent.left ← p.left;
else parent.right ← p.left;
}
else {
if (parent.left = p) then parent.left ← p.right;
else parent.right ← p.right;
}
}
else if (p.left ≠ null and p.right ≠ null) then { // ④ 삭제할 노드의 차수가 2인 경우
q ← maxNode(p.left); // 왼쪽 서브 트리에서 후계자 노드를 포인터 q로 지정
p.key ← q.key;
deleteBST(p.left, p.key); // 후계자 노드 자리에 대한 재구성
}
end deleteBST( )
'자료구조&알고리즘' 카테고리의 다른 글
| 균형 탐색 트리(AVL) (0) | 2022.03.10 |
|---|---|
| 히프(heap) (0) | 2022.03.10 |
| 재귀 함수(Recursive Function) (0) | 2022.03.04 |
| 재귀 호출(Recursion) (0) | 2022.03.03 |
| 힙(Heap)과 우선 순위 큐(Priority Queue) (0) | 2022.03.03 |