AVL 트리의 개요
1. AVL의 균형
1) 균형 인수(Balance Factor)
▪ 트리의 균형을 점검할 때 사용하는 인수
▪ 노드 마다 오른쪽 서브 트리의 높이에서 왼쪽 서브 트리의 높이를 뺀 것
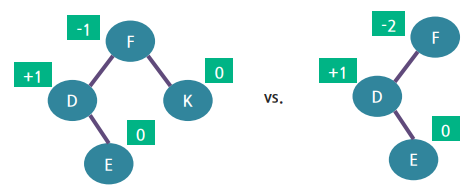
▪ AVL 트리에서 균형 인수의 값은 반드시 -1, 0, +1 중 하나임
2) 균형 인수의 점검
① 왼쪽 트리로부터 노드 K를 삭제하면 균형 인수 중 -2가 생겨 오른쪽 트리처럼 균형이 깨지게 됨
② 왼쪽 트리에서 노드 F의 오른쪽 자식에 삭제가 가해졌다면 루트 F를 기준으로 오른쪽 서브 트리의 높이가 감소하게 됨
③ 삭제로 인해 어떤 노드의 균형 인수가 범위를 벗어난 경우
: 균형이 깨진 노드는 삭제 위치의 부모 노드(F)의 왼쪽 자식 노드와 손자 노드까지 가는 길목에 있는 F, D, E 중에 존재하게 됨

2. AVL의 회전
1) 회전(Rotation)에 의한 균형 회복
▪ 불균형 노드의 위치를 기준으로 분류
- LL : 불균형 노드의 왼쪽 서브 트리의 왼쪽 서브 트리의 높이 증가
- LR : 불균형 노드의 왼쪽 서브 트리의 오른쪽 서브 트리의 높이 증가
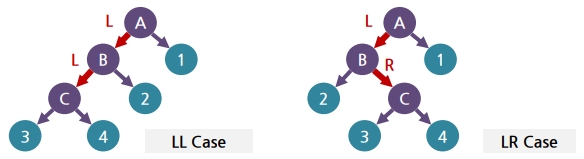
- RL : 불균형 노드의 오른쪽 서브 트리의 왼쪽 서브 트리의 높이 증가
- RR : 불균형 노드의 오른쪽 서브 트리의 오른쪽 서브 트리의 높이 증가

2) LL 회전 – 삽입에 의한 불균형 발생의 예
▪ 불균형 노드의 왼쪽 서브트리의 왼쪽 서브트리의 높이가 증가함
▪ LL의 RChild에 삽입되는 경우와 LChild에 삽입되는 경우가 있음
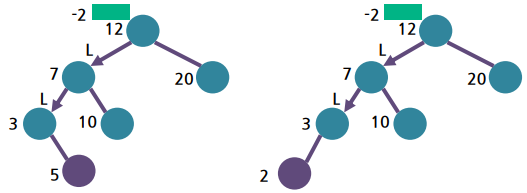
3) 균형 회복 과정 – 불균형 노드(루트 노드)

AVL 트리의 균형 조정 방법
1. AVL 트리의 균형
1) AVL의 개요
▪ 가장 먼저 시도된 이론
▪ 균형을 잡기 위해 트리 모습을 수정
▪ 실제 코딩 면에서 볼 때 AVL 트리는 매우 까다롭고 복잡
2) 트리 재구성의 장단점
▪ 탐색 효율 O(lgN)을 보장
▪ 삽입, 삭제 될 때마다 균형 파괴여부 검사하는 시간이 필요
▪ 트리를 재구성(Rebuilding)하는 시간이 필요
2. 균형 트리와 자체 조정 트리
1) 균형 트리(Balanced Tree)
▪ 최악의 경우에도 무조건 lgN 시간에 탐색(탐색 효율 보장)
▪ 루트로부터 리프까지 가는 경로를 최소화

2) 자체 조정 트리(Self-Restructuring Tree)
▪ 모든 노드가 동일한 빈도(Frequency)로 탐색되는 것이 아님
▪ 무조건 균형을 유지할 것이 아니라 자주 탐색되는 노드를 루트 근처에 갖다 놓는 것이 더욱 유리
3. 자체 조정 트리
1) 조정 방법Ⅰ- 특징
▪ 어떤 노드가 탐색될 때마다 그 노드를 바로 위 부모 노드로 올리는 방법
▪ 한번의 회전만으로 충분함