2-3트리
개요
- 2-3트리의 특징
▪ AVL은 균형 트리를 지향하는 반면 2-3 트리는 완전 균형 트리를 지향함
▪ AVL 트리에 비해 상대적으로 단순한 논리
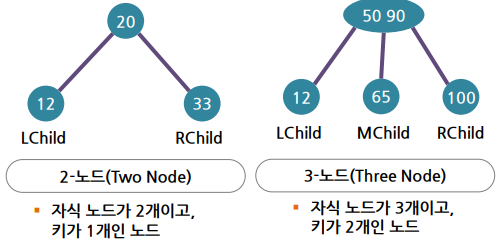

▪ 2-노드 또는 3-노드 모두 가능
▪ 이진 탐색 트리와 마찬가지로 리프 노드에 삽입
- 삽입 시 높이 변화의 특성
* 2-3트리
▪ 반복된 삽입에도 2-3 트리의 높이는 좀처럼 증가하지 않음
▪ 3-노드를 사용해서 최대한 많은 레코드를 높이 변화 없이 수용
* 이진 트리
▪ 이진 탐색 트리의 높이는 삽입할 때마다 리프 노드 아래로 1만큼 증가
- 여러 가지 방법
▪ 삽입, 삭제를 위해서는 삽입 대상 노드의 부모 노드를 접근해야 함
▪ 삽입 시에 중간 키를 올리기 위해서, 또 삭제 시에 부모 노드의 키를 아래로 내리기 위해서 이진 트리는 부모 노드로부터 자식 노드로 가는 포인터만 유지
▪ 루트로부터 내려가면서 만나는 모든 노드를 가리키는 포인터 값을 계속적으로 스택에 푸시해 놓으면 팝(Pop) 연산을 통해 직전의 부모 노드에 접근할 수 있음
- 탐색 효율
▪ 모든 노드가 3-노드일 때 가장 높이가 낮음
▪ 레벨 0의 루트 노드가 3노드라면 그 내부에는 2개의 레코드가 들어감
▪ 레벨 1에 3개의 3-노드가 있다면 그 내부에는 각각 2개의 레코드가 들어감
▪ 레벨 h까지의 레코드 수
N = 2(1 + 3 + 32 + ... + 3h) ≈ 3h
▪ 트리 높이 h는 최대 레벨 수와 일치하므로 결과적으로 h ≈ log3N
▪ 최악의 경우는 모든 노드가 2-노드로서 트리의 높이 h ≈ log2N
▪ 2-3 트리에는 2-노드와 3-노드가 섞여 있으므로 효율은 O(log2N)과 O(log3N) 사이에 존재함
▪ 이에 반해 이진 탐색 트리는 최악의 경우 O(N)으로 전락
▪ 2-3 트리는 항상 완전 균형 트리를 유지하므로 최악의 경우에도 효율을 보장
▪ 3-노드는 비교해야 할 키가 2개이므로 비교의 횟수가 증가
▪ 3-노드는 자식을 가리키는 포인터가 3개 이므로 자식 노드가 없다면 2-노드에 비해 널포인터가 차지하는 공간적 부담
▪ 널 포인터는 리프 노드에 다수가 분포