2-3-4 트리
1. 개요
- 2-3-4 트리의 정의
▪ O(log2N)과 O(log4N) 사이의 탐색 효율을 가짐
▪ 추가로 4-노드를 정의
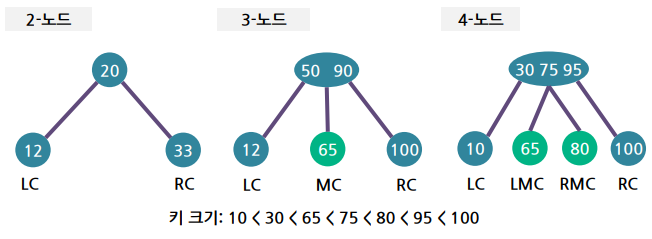
- 자식 노드로 가는 링크(Link)가 4개이고 키가 3개인 노드
- 왼쪽 자식(Left Child),
오른쪽 자식(Right Child),
왼쪽 중간 자식(Left Middle Child),
오른쪽 중간 자식(Right Middle Child)으로 구분
- 2-3-4 트리의 노드 구성
2. 2-3-4 트리의 필요성
1) 2-3-4 트리의 장단점
▪ 높이를 log4N으로 조금 더 낮추기 위함
▪ 리프 노드 근처의 널 포인터 공간도 2-3 트리에 비해서 더 많아짐
▪ 필요시 최대 3개의 키를 비교해야 하는 시간적 부담
2) 단일 패스 삽입
▪ 2-3 트리는 리프 노드가 꽉 찰 경우 → 중간 자식을 부모 노드로 올림
▪ 만약 부모 노드가 꽉 차면 → 다시 부모 노드의 중간 자식이 그 위로 올려짐
* 2-3-4 트리는 이러한 사태를 배제하기 위해 루트로부터 삽입 위치를 찾아서 내려가는 도중에 4-노드를 만나면 무조건 제거하면서 내려감
▪ 스택이 불필요
▪ 하나의 삽입 작업이 트리 모습을 바꾸면서 내려가는 동안, 동시에 이어서 두 번째 삽입 작업이 루트로부터 내려올 수 있음
* 파이프라이닝 (Pipelining) 방식
: 하나의 작업을 작은 단위로 나누고 다수의 파이프라인을 설정하여 여러 개의작업의 작은 단위들을 각 파이프라인에서 중첩한 뒤 동시에 처리하는 고전적 병렬처리 기법
3) 2-3-4 트리의 표현방법
▪ 레드블랙 트리로 구현

3. 삽입 시 4-노드의 제거


레드 블랙 트리
1. 레드 블랙 트리의 개요
1) 레드 블랙 트리(Red-Black Tree)란?
▪ 2-3-4 트리를 이진 트리로 표현한 것
▪ 레드 블랙 트리의 링크(Link)는 색깔을 지님
▪ 포인터 변수에 색깔이라는 속성을 추가

2) 노드 자료구조
▪ 키를 포함한 데이터 필드
▪ LChild 포인터, RChild 포인터
▪ LColor, RColor
▪ 색깔 변수 하나만 사용하려면 부모 노드로부터 자신을 향한 포인터의 변수를 표시
2. 레드 블랙 트리의 표현
1) 2-3-4의 RBT(Red Black Tree) 표현
▪ 모든 2-3-4 트리는 레드 블랙 트리로 표현 가능
▪ 2-노드는 그대로 둠

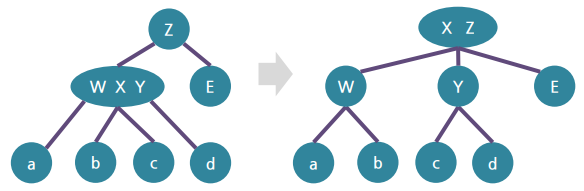
▪ 3-노드는 왼쪽 또는 오른쪽 키를 루트로 하는 이진 트리로 변경 → 따라서 트리 모양이 유일하지는 않음
▪ 빨강 링크는 원래 3-노드, 4-노드에서 같은 노드에 속했었다는 사실을 나타내며 4-노드의 레드 블랙 표현은 유일함

3. 레드 블랙 트리(Red-Black Tree)
1) 레드 블랙 트리의 속성
① 트리를 내려오면서 연속적인 빨강 링크 2개는 허용하지 않음
② 루트로부터 리프 노드까지 검정 링크의 수는 모두 동일함
③ 2개의 자식 노드가 모두 빨강 링크일 때만 4-노드에 해당함
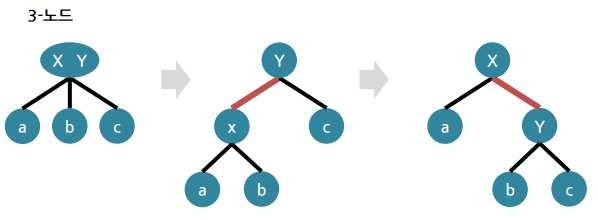
2) 속성 ① 트리를 내려오면서 연속적인 빨강 링크를 허용하지 않음
▪ 만약 첫 트리처럼 연속된 빨강이 존재한다고 가정하면 X-Y가 빨강이므로 그것은 둘째 트리에서 나왔을 것

▪ 그러나 셋째 트리의 4-노드는 항상 그 아래 트리처럼 유일한 모습의 레드 블랙 표현을 지님
▪ 따라서 연속적인 빨강이 2개 나올 수 없음
3) 사용 이유
▪ 2-3-4 트리의 복잡한 노드 구조와 복잡한 삽입 삭제 코드를 간결하게 표현하기 위함
▪ 레드 블랙 트리는 이진 탐색 트리의 함수를 거의 그대로 사용 가능함
▪ 2-3-4 트리의 장점인 단일 패스 삽입 삭제가 그대로 레드 블랙 트리에도 적용 가능함
▪ 언제 회전에 의해 균형을 잡아야 하는지가 쉽게 판별됨
'자료구조&알고리즘' 카테고리의 다른 글
| 다차원검색트리(KD-트리, KDB-트리, R-트리) (0) | 2022.07.05 |
|---|---|
| 선택/버블 정렬 (0) | 2022.03.15 |
| 2-3트리 (0) | 2022.03.15 |
| 균형 탐색 트리(AVL) (0) | 2022.03.10 |
| 히프(heap) (0) | 2022.03.10 |