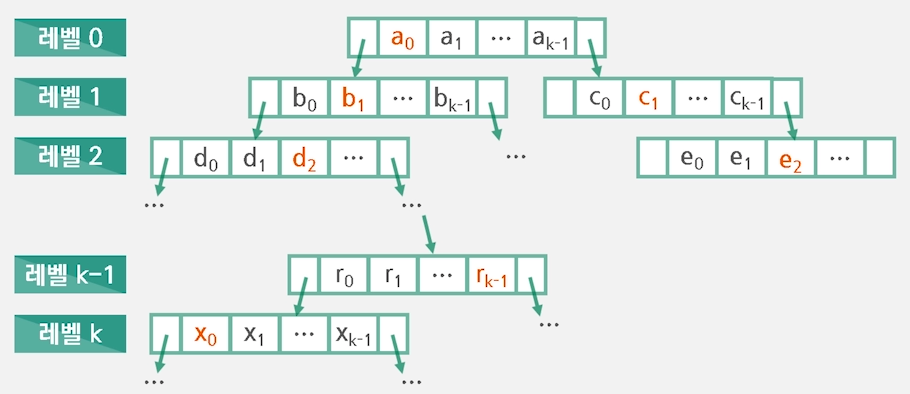
KD-트리
1) 이진검색트리를 확장
· k(k≥2)의 필드로 이루어진 키 사용
· 각 레벨에서 필드를 번갈아가며 검색에 사용
- 한 레벨에서는 하나의 필드만 사용
- 총 k개의 필드를 사용하는 검색이라면, k개의 레벨을 내려가면 검색에 사용하는 필드가 일치

- 기준 노드의 값과 비교 노드의 값으로 노드의 위치를 결정
- A의 x값을 기준으로 B는 왼쪽, C는 오른쪽에 위치
- B의 y값을 기준으로 D는 왼쪽, E는 오른쪽에 위치
- C의 y값을 기준으로 F는 오른쪽에 위치(크거나 같을 경우라면)
- D의 x값을 기준으로 G는 왼쪽에 위치
2) KD-트리 검색
- 임의의 키가 입력되면, 각 필드를 차례대로 사용해서 트리를 검색
3) KD-트리 삽입
- 검색하듯이 트리를 따라 내려가다 리프 노드를 만나면 거기에서 왼쪽 또는 오른쪽에 매달아 줌
4) KD-트리 삭제
- 자식이 없는 경우:
이진검색트리와 마찬가지로 노드 r만 제거
- 자식이 하나뿐인 경우:
자식 노드를 루트로 하는 서브트리가 한 레벨 위로 이동하므로 분기에 사용하는 필드가 달라짐(자식이 둘인 경우의 삭제와 동일)
- 자식이 둘인 경우:
오른쪽 서브트리 중 노드 r에서 분기에 사용한 필드의 값이 가장 작은 노드를 찾아 삭제하고 그 노드를 노드 r 자리로 이동
KDB-트리
# KD-트리와 B-트리의 특성 결합
- KD-트리의 특성의 다차원 key
- B-트리의 디스크 한 페이지가 한 노드와 일치, 균형잡힌 트리
1) 각 레코드는 k차원 공간에서 하나의 점에 해당함
- 자신이 속한 공간을 담당하는 색인 노드들을 따라감
2) 노드의 종류
- 영역 노드
ㄴ 복수 개의(영역, 페이지 번호) 쌍으로 구성
ㄴ 모든 내부 노드(Internal Node)는 영역 노드임
- 키 노드
ㄴ 복수 개의(키, 페이지 번호) 쌍으로 구성
ㄴ 모든 리프 노드는 키 노드임
3) KDB-트리 삽입(B-트리와 유사)
(1) 삽입할 키가 속하는 리프 노드 찾음
(2) 해당 리프 노드에 키를 더 수용할 수 있는 공간이 있으면 쌍을 삽입
(3) 수용할 수 없을 때 형제 노드와 재분배할 수 있으면, 재분배를 함
(4) 수용할 수 없을 때 형제 노드와 재분배할 수 없으면, 리프 노드를 분할하여 두 개의 영역을 만듦

3) KDB-트리 삭제(B-트리와 유사)
(1) 삭제 후 언더플로우가 생기지 않으면 작업 끝
(2) 언더플로우가 생기면 이웃 영역과 경계를 재조정해서 재분배할 수 있으면 재분배하고 작업 끝
(3) 언더플로우가 생겼을 때 재분배가 가능하지 않은 경우 병합
* 병합은 부모 노드에서 (영역, 페이지 번호) 쌍 두 개가 하나로 통합 → 재귀 상황
R-트리
1) KDB-트리에서는 노드들이 전체 공간을 나누어 커버하는 반면 R-트리는 키들을 모두 포함하는 최소 영역만 노드에 있음
- B-트리의 다차원 확장
- 균형잡힌 검색트리
- 모든 레코드는 리프 노드에서만 가리킴
- 다차원 도형의 저장 가능
ㄴ 점, 선, 면, 폐공간, 각종 도형
ㄴ MBR(Minimum Bounding Rectangle)로 근사
2) 노드의 종류
- KDB-트리와 동일
3) R-트리의 성질
- 루트를 제외한 모든 내부 노드는 k / 2의 내림 값~ k개의 영역을 가짐
- 모든 리프노드는 같은 깊이를 가짐
- 모든 레코드는 리프 노드에서만 가리킴

4) 레코드들과 R-트리의 관계

- 여기서 M과 N을 R7에 삽입하게 되면 오버플로우가 발생하여 재분배를 함
- R6에 M을, R7에 N을 삽입
cf) 그리드 파일
1) 검색트리 아님
2) 키의 내용에 의해 레코드가 저장된 곳을 '단번에' 알아낼 수 있도록 설계된 다차원 저장, 검색 수단
- 공간을 서로 베타적인 격자(그리드) 영역으로 나눈 다음 해당 영역에 속하는 레코드들을 모아서 자장함으로써 임의의 레코드에 대한 저장과 검색을 단번에 할 수 있음

- 페이지에 저장하며, 페이지에 오버플로우가 발생 시 분할하여 저장
예) P1(페이지)에 [a, b, c]가 저장되어 있는 상태에 d를 삽입하려면 P1의 오버플로우가 발생, 따라서 P2를 생성하여 P1의 c와 삽입할 d를 P2에 저장