유향 비순환 그래프(Directed Acyclic Graph, DAG)
- 순환이 없도록 설계된 방향성을 가진 그래프이다.
- 즉 어떤 정점이든 1회만 접근 가능하도록 비순환적(Acyclic)으로 만들어진 그래프이다.
- 수학, 컴퓨터, 과학 등 여러분야에서 사용하는 용어이며, 높은 처리량에 우수하여 사물 인터넷과 소액 결제와 같은 많은 영역에서 활용될 수 있다.
- 따라서 어떤 선행되어야 하는 것이 있는 경우를 표현할 때 유용하다.
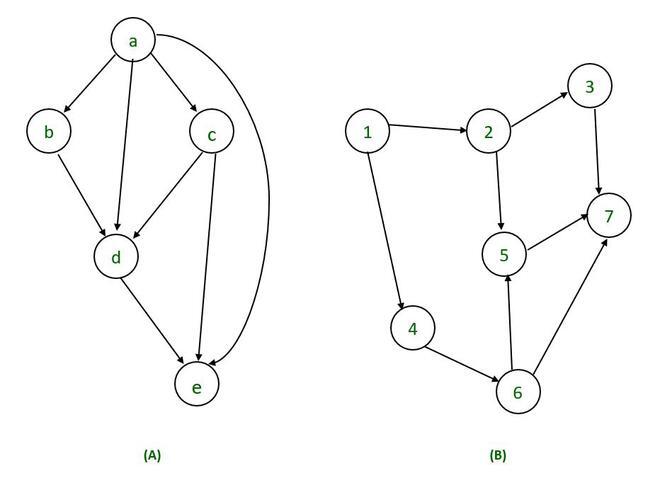
위상정렬(Topological Sort)
- DAG의 정점들을 순서화하기 위한 정렬, 즉 DAG 위에서만 동작 가능
- 우선순위를 표현하기 위해 사용하는 정렬 알고리즘
- 일반적으로 시간복도는 O(V + E)를 갖는다.
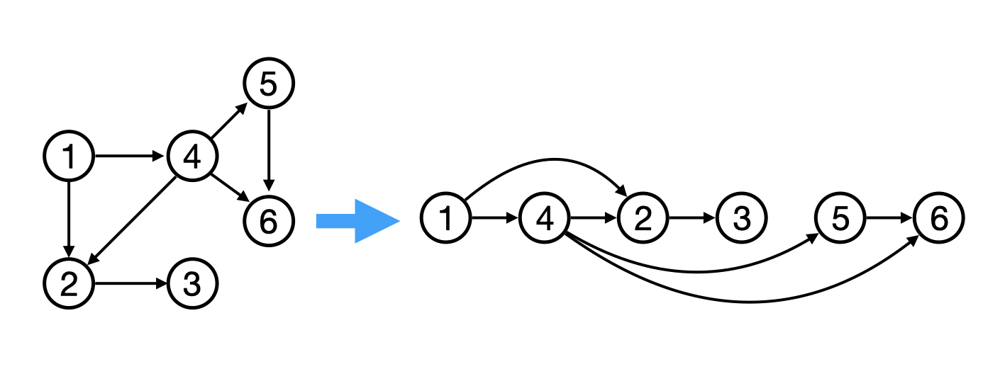
DAG를 활용한 최단경로, 최장경로
- 위상순서 위에 DAG는 최단경로 문제를 효율적으로 해결 가능할 수 있다.
- 단일 정점 최단경로 알고리즘 중 하나인 다익스트라 알고리즘은 O(E x logV)의 시간복잡도를 갖지만, 위상정렬을 활용한 DAG는 O(V + E)의 시간복잡도를 갖기 때문에 보다 효율적으로 최단 경로 문제를 해결 가능하게 한다.
동작
1) 먼저 DAG에서 위상정렬을 통해 위상순서를 구함
2) 최단 거리를 저장할 배열을 정의 후 양의 무한대 값으로 초기화
3) 시작 정점에 대한 최대거리는 0으로 초기화
4) 위상순서대로 정점을 방문하여 정점까지의 거리와 연결된 간선의 거리를 합한 값으로 다음 정점까지의 거리를 갱신
이미 저장된 최단거리 값이 있다면, 새로 계산된 거리의 값이 더 작은 경우에만 값을 갱신
ref)
1) https://en.wikipedia.org/wiki/Directed_acyclic_graph
Directed acyclic graph - Wikipedia
From Wikipedia, the free encyclopedia Jump to navigation Jump to search Directed graph with no directed cycles Example of a directed acyclic graph In mathematics, particularly graph theory, and computer science, a directed acyclic graph (DAG ) is a directe
en.wikipedia.org
2) https://academy.binance.com/ko/articles/what-is-a-directed-acyclic-graph-dag-in-cryptocurrency
암호화폐에서 방향성 비순환 그래프(DAG)란 무엇인가요? | Binance Academy
방향성 비순환 그래프(DAG)는 암호화폐 블록체인의 대안으로 제시된 데이터 구조입니다. 바이낸스 아카데미에서 자세히 알아보시기 바랍니다.
academy.binance.com
3) https://github.com/williamfiset/Algorithms
GitHub - williamfiset/Algorithms: A collection of algorithms and data structures
A collection of algorithms and data structures. Contribute to williamfiset/Algorithms development by creating an account on GitHub.
github.com